算法源码地点：https://github.com/wudashan/longest-path-problem

媒介

最近产物线举行了一个软件编程大赛，题目很是的有趣，就是在一个9 × 9的格子里，你要和另一个仇人PK，在PK的进程中，你可以吃格子里的果实来晋升进攻力。每次可以往正上、正下、正左、正右、左上、左下、右上、右下八个偏向走。每次要么持续吃果实要么持续走空缺区域，且不能走反复的位置。初始状态如下图所示：

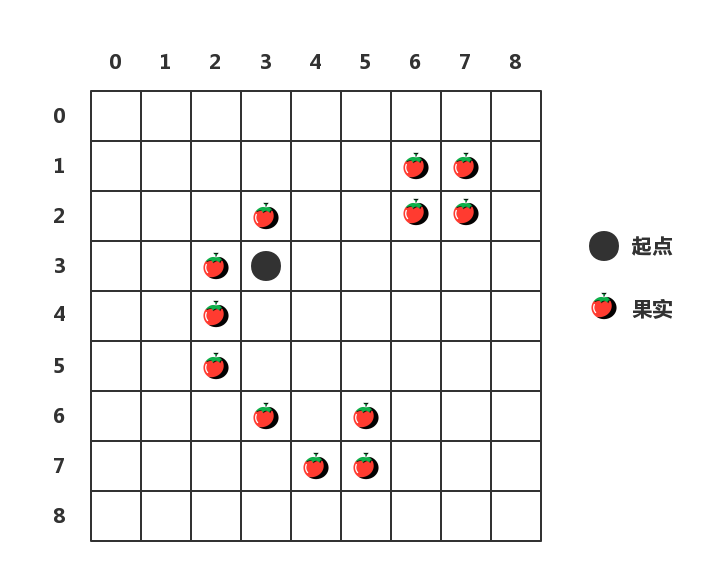
为了晋升进攻力，我们需要尽大概地一次吃最多的果实，所以蹊径可以这样筹划：

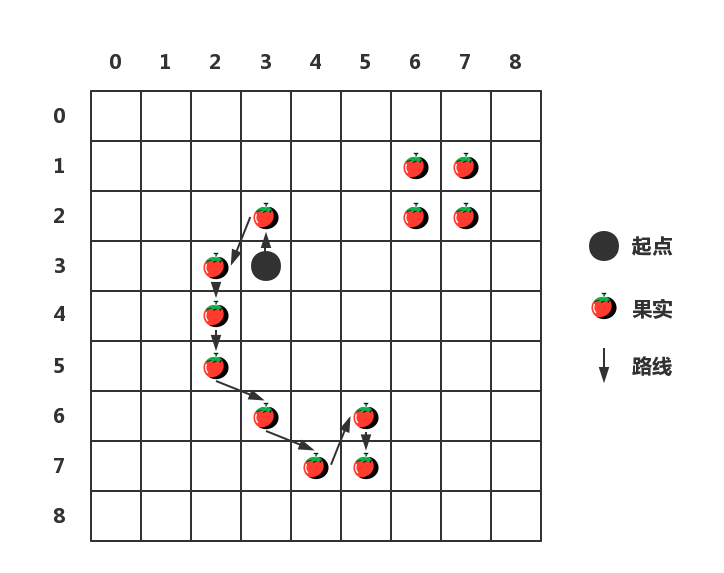
至此，我们可以对这个问题举办描写：已知空缺区域不能走，每次可以往正上、正下、正左、正右、左上、左下、右上、右下八个偏向走，走过的位置不能再走，求能吃最多果实的蹊径（最长路径问题）？

前置条件

舆图暗示

首先我们将上面的舆图利用布尔范例的二维数组暗示，个中true暗示可以行走的格子，false暗示不能行走的格子：

boolean[][] simpleMap = new boolean[][] {
    {false, false, false, false, false, false, false, false, false},
    {false, false, false, false, false, false, true , true , false},
    {false, false, false, true , false, false, true , true , false},
    {false, false, true , false, false, false, false, false, false},
    {false, false, true , false, false, false, false, false, false},
    {false, false, true , false, false, false, false, false, false},
    {false, false, false, true , false, true , false, false, false},
    {false, false, false, false, true , true , false, false, false},
    {false, false, false, false, false, false, false, false, false}
};

格子暗示

对付舆图上的每一个格子，我们用一个简朴类来暗示：

public class Pos {

    private int x;  // 横坐标
    private int y;  // 纵坐标
    
    // get、set、construct要领省略

    @Override
    public String toString() {
        final StringBuffer sb = new StringBuffer("Pos{");
        sb.append("x=").append(x);
        sb.append(", y=").append(y);
        sb.append('}');
        return sb.toString();
    }

    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass()) return false;

        Pos pos = (Pos) o;

        if (x != pos.x) return false;
        return y == pos.y;
    }

    @Override
    public int hashCode() {
        int result = x;
        result = 31 * result + y;
        return result;
    }

    
}

由于我们是利用横纵坐标而不是几行几列来暗示一个格子（没错，我就是这么傲娇），那么我们就需要给舆图界说横纵坐标偏向。偏向如下图所示：

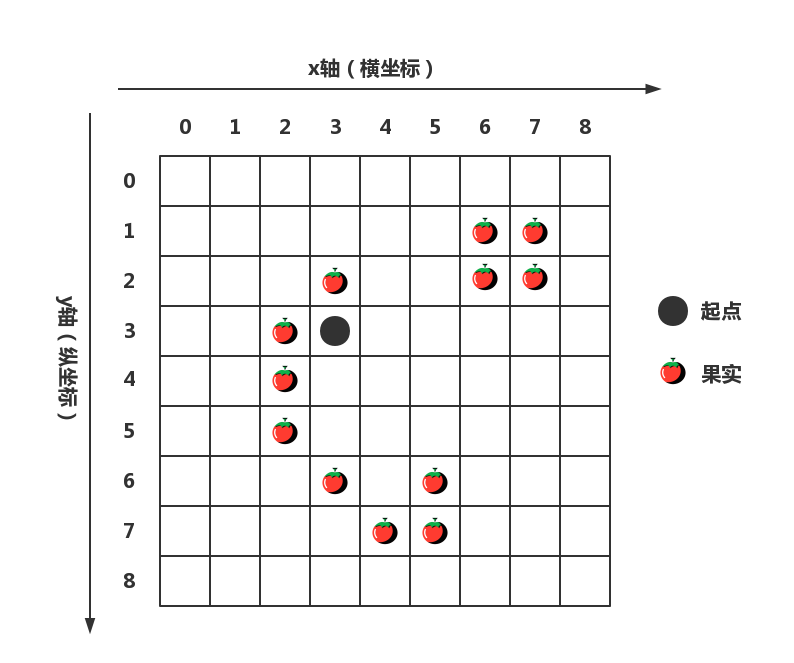
那么起点上方的果实坐标就是[3, 2]（横坐标为3，纵坐标为2），可是对应着二维数组为map[2][3]（第二行，第三列），软件开发，即横坐标对应着二维数组的列，纵坐标对应着二维数组的行。

移动暗示

为了措施简捷，我们给八个偏向的移动界说对应的偏移量，这样每次行走只要对偏移量数组举办for轮回就可以了。

Pos[] moveOffset = new Pos[] {
    new Pos(-1,  0),    // 向左移动
    new Pos(-1, -1),    // 向左上移动
    new Pos( 0, -1),    // 向上移动
    new Pos( 1, -1),    // 向右上移动
    new Pos( 1,  0),    // 向右移动
    new Pos( 1,  1),    // 向右下移动
    new Pos( 0,  1),    // 向下移动
    new Pos(-1,  1)     // 向左下移动
};

深度优先搜索算法

算法思想

拿到这道题，脑壳里第一个想到的就是深度优先搜索算法，其思想为每次往八个偏向递归，当不能继承走下去的时候生存最长路径，软件开发，并回退到能继承行走的格子，继承递归直到竣事。

代码示例

接下来就是我们的深度优先搜索代码：

/**
 * 通过深度优先搜索算法获取最长路径
 * @param map 舆图
 * @param start 起点
 * @param moveOffset 移动偏移量
 * @return 最长路径
 */
public static List<Pos> getLongestPathByDFS(boolean[][] map, Pos start, Pos[] moveOffset) {

    List<Pos> longestPath = new ArrayList<>();
    dfs(start, map, new ArrayList<>(), longestPath, moveOffset);
    return longestPath;

}

/**
 * 递归实现深度优先搜索
 */
private static void dfs(Pos pos, boolean[][] map, List<Pos> path, List<Pos> result, Pos[] moveOffset) {

    // 记录当前位置向周围格子移动的记录
    List<Pos> visited = new ArrayList<>();

    // 生存当前位置的周围格子
    Pos[] neighbours = new Pos[moveOffset.length];

    // 依次向周围移动
    for (int i = 0; i < moveOffset.length; i++) {
        Pos next = new Pos(pos.getX() + moveOffset[i].getX(), pos.getY() + moveOffset[i].getY());
        neighbours[i] = next;
        if (inMap(map, next) && !path.contains(next) && map[next.getY()][next.getX()]) {
            path.add(next);
            visited.add(next);
            dfs(next, map, path, result, moveOffset);
        }
    }

    // 若在当前位置下，没有向周围的格子移动过期，生存最长路径
    if (visited.isEmpty()) {
        if (path.size() > result.size()) {
            result.clear();
            result.addAll(path);
        }
    }

    // 周围的格子都不行以移动时回退到上一格子
    for (Pos neighbour : neighbours) {
        if (canPath(map, path, neighbour, visited)) {
            return;
        }
    }
    path.remove(pos);

}

/**
 * 判定格子是否可以移动
 */
private static boolean canPath(boolean[][] map, List<Pos> path, Pos pos, List<Pos> visited) {

    // 不在舆图里，不能移动
    if (!inMap(map, pos)) {
        return false;
    }

    // 空缺格子，不能移动
    if (!map[pos.getY()][pos.getX()]) {
        return false;
    }

    // 已经在路径中或颠末，不能移动
    if (path.contains(pos) || visited.contains(pos)) {
        return false;
    }

    return true;
}

/**
 * 判定格子是否在舆图内
 */
private static boolean inMap(boolean[][] map, Pos pos) {

    if (pos.getY() < 0 || pos.getY() >= map.length) {
        return false;
    }

    if (pos.getX() < 0 || pos.getX() >= map[0].length) {
        return false;
    }

    return true;

}