WARNING:这是七年前的一篇文章…这个要领不合用于大量数据，仅仅是提供一种利用SVD的思路.

某天，一群《Family Guy》的粉丝们聚在一起，抉择建设一个网站来分享各自喜欢的电视和对他们的评分，不久之后他们就得到了一个不错的网站，然后又有一大群人簇拥而至和他们一起评分、分享，相互推荐电视剧集. 但由于用户越来越多，逐个查察某小我私家的评分记录，给她推荐影戏越来越费事儿. 于是有人提出应该利用所有人的集团伶俐来为每一个单独的人提供发起，这个进程应该是自动化的.

是不是看起来很熟悉？没错，这就是推荐系统的雏形.此刻已经有了无数的论文描写如何通过巨大的算法来实现推荐系统，但今朝为止最有效、最常用同时也是最简朴的要领是: 奇异值解析(SVD), 也常被用于潜在语义索引和降维处理惩罚.

线性代数配景常识

SVD的配景常识可以简朴描写为以下内容：

任何一个MxN的矩阵A，假如它的行数M大于或便是它的列数N，那么它就可以被转换成以下三个矩阵的乘积:一个MxM的正交矩阵U, 一个MxN的对角矩阵W(奇异值矩阵), 和一个正交矩阵V的转置矩阵.

更直观的说，假如我们有一个矩阵，每一行代表一个产物, 每一行中的所有用户对该产物的评分. 因此我们有了M个产物，N个用户的矩阵MxN.按照上面的理论，劳务派遣管理系统，我们可以把这个矩阵解析为 MxM 的矩阵U, MxN 的奇异值矩阵S和 NxN 的矩阵V. 最棒的是，我们可以通过S矩阵的前几个奇异值就可以靠近本来的MxN的矩阵了，而不必取完整的S(数学道理).

与呆板进修的干系

呆板进修最根基的一项成果就是用少量的字节尽大概靠近的暗示大量数据（如用户的聚类等）.SVD正好给我们提供了通过少两字节暗示大数据的成果，方法就是把数据投影到更小的维度上.

SVD最初在LSI(潜在语义索引)上大量利用，在这种场景下，每一行暗示一个文档，行中的所有列暗示每一个词.通过SVD我们可以可以找到那些关联度较量大的项(好比那些常常同时呈现的词),把这些关联度较量大的词作为一个特征(这就到达了降维的目标).最终的目标就可以把那些不重要的噪声去掉，只保存有用的信息.实践中做信息检索的人凡是会把10000+的维度降到几百. 同样的要领也可以用在图像压缩和计较机视觉应用上.

降维

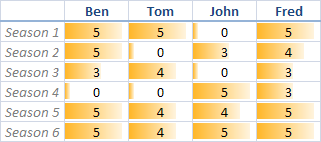
回到我们最初的电视剧问题.简朴起见，我们用6个电视剧剧集和4个用户构成矩阵(6×4矩阵).然后把这个矩阵利用SVD解析成三个小矩阵,U(6×6), S(6×4), V(4×4),为了简朴起见，我们只取每个矩阵的前两列:

此刻我们有了二维的数据，可以把功效画出来了. 我们把U的第一列作为x轴，第二列作为y轴可以画出差异的电视剧集的漫衍图.同样可以画出V的漫衍以暗示用户的漫衍.

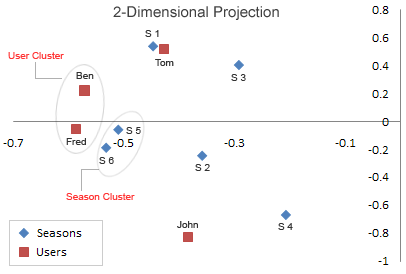
我们可以看到两个用户很是像(虽然用户太少，称他们为cluster有点言过其实)，当用户越来越多的时候聚类就越来越明明.从图中我们可以看出Ben和Fred的咀嚼很像.

找到相似用户

此刻，新用户Bob进来了，然后对一些剧集做了评分([5,5,0,0,0,5] for seasons 1-6) – 我们此刻需要按照这些新数据给他做推荐.直观上来看，我们需要找到跟Bob相似的用户, 假如我们能把Bob插入到我们的二维空间，软件开发，就可以找到谁跟他相似了，为了实现这点，我们需要举办以下的计较：

通过简朴地矩阵计较，软件开发，我们就可以把Bob投影到二维空间，详细的数学道理可以在上面提到的线性代数参考资料中看到. 此刻我们把Bob添加到我们的图中:

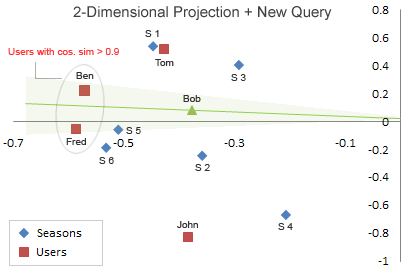
此刻我们就可以通过一系列相似性算法，如余弦相似度来计较Bob与谁最靠近了.通过余弦相似度我们发明Ben与Bob最靠近.